Answer:
a) The ball clears the crossbar by 0.75 m.
b) The ball cleared the crossbar while falling.
c) The final velocity of the ball when it reaches the goal post is
v = (12, -13) m/s (component form)
v = (18 m/s, -48°) (polar coordinates)
Step-by-step explanation:
Hi there!
The velocity and position vectors of the ball can be calculated using the following equations:
r = (x0 + v0 • t • cos α, y0 + v0 • t • sin α + 1/2 • g • t²)
v = (v0 • cos α, v0 • sin α + g • t)
Where:
r = position vector at time t.
x0 = initial horizontal position.
v0 = initial velocity.
α = launching angle.
y0 = initial vertical position.
t = time.
g = acceleration due to gravity (-9.8 m/s² considering the upward direction as positive)
v = velocity vector at time t.
Please, see the attached figure for a better understanding of the problem.
The vector r1 in the figure is the position vector the ball must have to clear the crossbar. When the x-component of the position vector is 36 m, the y-component must be at least 3.05 m to clear the crossbar. Using the equation of the x-component of the position vector, let´s find the time at which the ball traveled 36 m horizontally.
r1x = x0 + v0 • t • cos α
Let´s place the origin of the frame of reference at the kicking point so that x0 and y0 = 0.
r1x = v0 • t • cos α
36 m = 20 m/s · t · cos 53°
36 m / (20 m/s · cos 53°) = t
t = 3.0 s
Now let´s see if the y-component of the position vector is at least 3.05 at t = 3.0 s
r1y = y0 + v0 • t • sin α + 1/2 • g • t² (y0 = 0)
r1y = v0 • t • sin α + 1/2 • g • t²
r1y = 20 m/s · 3.0 s · sin 53° - 1/2 · 9.8 m/s² · (3.0 s)²
r1y = 3.8 m
It´s a goal! When the ball travels the 36 m to the goal its height is 3.8 m. The ball clears the crossbar by (3.8 m - 3.05 m) 0.75 m.
b) To answer this question, let´s calculate the vertical component of the velocity at t = 3.0 s. If it is negative, then the ball cleared the crossbar while falling, if it is positive the ball cleared the crossbar while rising. Look in the figure the vectors v2 and v3. v2 is a velocity vector of the ball while rising. Notice that the y-component of v2 (v2y) is positive (upward direction). In change, v3 is a velocity vector of the ball while falling. The y-component of v3, v3y, is directed downward, then, it is negative.
The vertical component of the velocity vector at t = 3.0 s will be:
v1y = v0 • sin α + g • t
v1y = 20 m/s · sin 53° - 9.8 m/s² · 3.0 s
v1y = -13 m/s
The y-component of the velocity vector is negative, then, the ball cleared the crossbar while falling.
c) Let´s use the equation of the velocity vector. The y-component of the velocity at t =3.0 s was already calculated above in part b).
v1x = v0 • cos α
v1x = 20 m/s · cos 53°
v1x = 12 m/s
Then, the velocity vector when the ball reaches the goal post is
v1 = (12, -13) m/s
On polar coordinates, we have to find the angle θ (see he vector v1 in the figure) and the magnitude of v1.
v1 = (magnitude, θ)
The magnitude of v1 is calculated as follows:
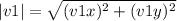
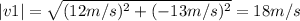
The magnitude of v1 is 18 m/s
To find θ, we have to use trigonometry of right triangles:
cos θ = adjacent side / hypotenuse
or
sin θ = opposite side / hypotenuse
In this case, the triangle is formed by v1, v1x, and v1y. v1 is the hypotenuse, v1x is the side adjacent θ and v1y is the opposite side (see attached figure).
Then:
cos θ = v1x/v1
cos θ = 12 m/s / 18 m/s
θ = 48°
Since the angle is below the horizontal it will be -48°
Then, on polar coordinates the velocity vector v1 will be: v1 = (18 m/s, -48°).