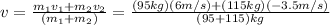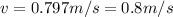Question

The football players collide head-on in midair while trying to catch a thrown football. The first player is 95.0 kg and has an initial velocity of 6.00 m/s, while the second player is 115 kg and has an initial velocity of –3.50 m/s. What is their velocity just after impact if they cling together?

Answer 1

`v=0.8m/s`

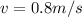
Step-by-step explanation:

To solve the problem, we can use collisions theory from classical physics

If we analyze the players before and after the collision we got:

`p_(1)=p_(2)`

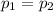
Since the cling together

`m_(1)v_(1)+m_(2)v_(2)=(m_(1)+m_(2))v`

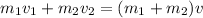
From the exercise we know that the first player is 95.0 kg and has an initial velocity of 6.00 m/s, while the second player is 115 kg and has an initial velocity of –3.50 m/s.

`v=(m_(1)v_(1)+m_(2)v_(2))/((m_(1)+m_(2)))=((95kg)(6m/s)+(115kg)(-3.5m/s))/((95+115)kg)`

`v=0.797m/s=0.8m/s`