Question

Write the summation to estimate the area under the curve y=2+√x from x=2 to x=5 using 3 rectangles and right endpoints.

Answer 1

11.968 square units.

Explanation:

The given equation of the curve is

`y=2+√(x)`

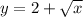
We need to write the summation to estimate the area under the given curve from x=2 to x=5 using 3 rectangles and right endpoints.

End points are : 2,3,4,5

Right end points are : 3,4,5

Find the value of the function at x=3,4,5.

At x=3,

`y=2+√(3)`

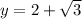
At x=4,

`y=2+√(4)=2+2=4`

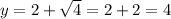
At x=5,

`y=2+√(5)`

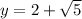
The area of under the curve is

`Area=\sum_(k=2)^5 \Delta xf(x_(k+1)})`

`Area=1\cdot (2+√(3))+1\cdot (4)+1\cdot (2+√(5))`

`Area=2+√(3)+4+2+√(5)`

`Area=8+√(3)+√(5)`

`Area\approx 11.968`

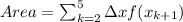
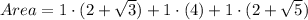
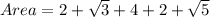
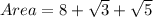
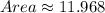
Therefore, the area under the curve 11.968 square units.