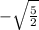Answer:
Explanation:
There are 6 solutions or zeros here because, according to the Fundamental Theorem of Algebra, the degree of the polynomial dictates how many zeros there are in the polynomial. If we had a 3rd degree polynomial, we would expect to find 3 zeros; if we had a 5th degree polynomial, we would have 5 zeros, etc. The easiest way to factor this is to do it initially by grouping:
 then
then
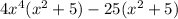 then
then
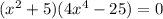
We will factor each set of parenthesis now to get all the zeros. For the first set of parenthesis:
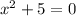 so
so
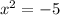 so
so

But since we can't have a negative under the square root, we have to offset it by using the imaginary number i. i-squared = -1, so
x = ±i√5
Those are the first 2 zeros out of 6. Now for the second set of parenthesis:
4x⁴ - 25 = 0. That is the difference between perfect squares, and that factors to this:
(2x² + 5)(2x² - 5)
The first set of parenthesis there:
2x² + 5 = 0 so
2x² = -5 so
x² = -5/2 so
x = ±
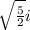
Those are the next 2 zeros. We found 4 so far, now we will find the last 2 in the second set of parenthesis above:
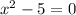 so
so
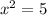 so
so
x = ±
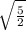
In summary, the 6 zeros are as follows:
x =
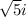 , -
, -
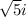 ,
,
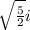 ,
,
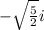 ,
,
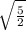 ,
,