Question

While driving north at 25 m/s during a rainstorm you notice that the rain makes an angle of 38° with the vertical. While driving back home moments later at the same speed but in the opposite direction, you see that the rain is falling straight down. From these observations, determine the speed and angle of the raindrops relative to the ground.

Answer 1

Answer:
`21.33^(\circ)`

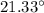
Step-by-step explanation:

Given

velocity of driver
`v_1`=25 m/s w.r.t ground towards north

driver observes that rain is making an angle of
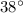`38^(\circ)` with vertical

While returning
`v_2`=25 m/s w.r.t. ground towards south

suppose
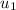`u_1`=velocity of rain drop relative car while car is going towards north

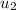`u_2`=velocity of rain drop relative car while car is going towards south

z=vector sum of
`u_1 & v_1`

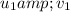
Now from graph

`\tan 38=(v_1+v_2)/(u_2)`

`u_2=(25+25)/(\tan 38)=64 m/s`

`z=\vec{u_2}+\vec{v_2}`

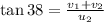
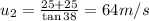
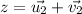
therefore magnitude of z is given by

`|z|=√(u_2^2+v_2^2)`

`|z|=√(64^2+25^2)`

`|z|=68.70 m/s`

`\tan A=(v_2)/(u_2)`

`\tan A=(25)/(64)=0.3906`

`A=21.33^(\circ)`

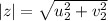
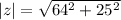
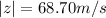
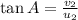
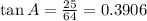
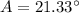
Thus rain drops make an angle of
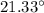`21.33^(\circ)` w.r.t to ground