Answer:
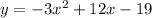
Explanation:
we know that
The quadratic equation in standard form is equal to
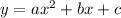
we have
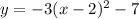
This is a quadratic equation in vertex form
Convert to standard form
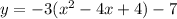
Apply distributive property
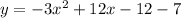
Combine like terms
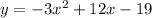 ----> quadratic equation in standard form
----> quadratic equation in standard form