Question

How many 5-digit sequences can we form from the integers 1, 2, ..., 9 if:

a) the digits can be the same.
b) the digits cannot be the same and the order in which they appear matters.
c) the digits cannot be the same and the order in which they appear does not matter

Answer 1

Answer: a) 59049, b) 15120, c) 126.

Explanation:

Since we have given that

5 digit sequences from the integers 1,2,...9.

a) the digits can be the same.

Repetition is allowed.

So, Number of ways to form 5 digit sequences would be

`9* 9* 9* 9* 9\\\\=9^5\\\\=59049`

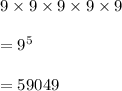
b) the digits cannot be the same and the order in which they appear matters.

Repetition is not allowed and order is maintained, so we will use "Permutation":

`^9P_5=15120`

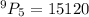
c) the digits cannot be the same and the order in which they appear does not matter.

Repetition is not allowed and order is not maintained, so we will use "Combination":

`^9C_5=126`

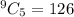
Hence, a) 59049, b) 15120, c) 126.