Question

produces decorative mailboxes. The​ company's average cost per unit is $ 23.43 when it produces 1 comma 400 mailboxes. Requirements 1. What is the total cost of producing 1 comma 400 ​mailboxes? 2. If $ 20 comma 202 of the total costs are​ fixed, what is the variable cost of producing each​ mailbox? 3. Write Rollins Mailbox​'s cost equation. 4. If the plant manager uses the average cost per unit to predict total​ costs, what would the forecast be for 1 comma 500 ​mailboxes? 5. If the plant manager uses the cost equation to predict total​ costs, what would the forecast be for 1 comma 500 ​mailboxes? 6. What is the dollar difference between your answers to questions 4 and​ 5? Which approach to forecasting costs is​ appropriate? Why?

Answer 1

1) The total cost of production (TC) is $32,802.

2) The variable cost per unit is $9/unit.

3) Cost equation:
`TC(Q)=20,200+9Q`

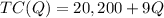
4) TC=$35,145

5) TC=$33,702

6) Difference=$1,443

The appropiate approach is using the cost function, because its differentiates the cost that are fixed and not dependant of the volume of production, and the variable cost, that are proportional to the quantity produced.

Step-by-step explanation:

1) The total cost of production can be calculated as the product of the cost per unit ($23.43/unit) and the total ammount of units (1,400 units):

`TC=c*Q=23.43*1,400=32,802`

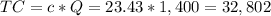
The total cost of production (TC) is $32,802.

2) The fixed cost (FC) are $20,202, so the variable cost are:

`VC=TC-FC=32,802-20,202=12,600`

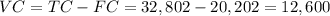
This is the variable cost for 1,400 mailboxes, so the unit variable cost is:

`vc=VC/Q=12,600/1,400=9`

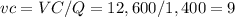
The variable cost per unit is $9/unit.

3) The equation of cost can be written as:

`TC(Q)=20,200+9Q`

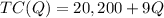
4) If it uses the average cost tot predict the cost of 1,500 mailboxes, he will get:

`TC=23.43*1,500=35,145`

5) If he uses the cost function, he will get

`TC=20,202+9*1500=20,202+13,500=33,702`

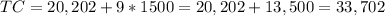
6) The dollar difference between the two estimates is:

`TC_4-TC_5=35,145-33,702=1,443`

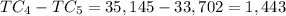
The appropiate approach is using the cost function, because its differentiates the cost that are fixed and not dependant of the volume of production, and the variable cost, that are proportional to the quantity produced.

The average cost per unit is not constant for every quantity and the error will increase if the quantity is much different from 1,300 units.