Question

Two boxes are connected to each other by a string as shown in the figure. The 10-n box slides without friction on the horizontal table surface. The pulley is ideal and the string has negligible mass. What is true about the tension t in the string?

Answer 1

T < 30N

Step-by-step explanation:

According to the figure, we have a system with 2 blocks attached by a string which passes through a pulley. In this case, we have to use Newton't law to find the tension of the string. We need to analyse each block to know what vertical and horizontal forces are present in each of them.

10N block:

Horizontal forces: Tension (T).

Vertical forces: Weight (W).

There's no friction and knowing this values, we can find the mass using:
`W = mg`.

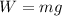So,
`m = (W)/(g) = (10)/(9.8) =1.02 kg`.

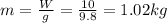30N block:

There's no horizontal forces because the block is suspended.

Vertical forces: Tension and Weight.

We can calculate the mass using
`W = mg`

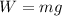
So,
`m = (W)/(g) = (30)/(9.8) = 3.06 kg`.

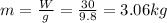Now, we analyse the system, to do so, we need to express vertical forces interactions and horizontal forces interactions:

According to second Newton's Law
`\sum F = ma`.

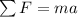So, vertically for 30N block:
`\sum F_(y) = W_(30) - T=ma`

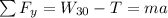
Then, horizontally for 10N block:
`\sum F_(x)= T = ma`

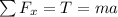
So,
`\left \{ {{W_(30) -T=m_(30) a} \atop {T=m_(10) a}} \right.`.

Now we have to solve this system replacing a from the second equation into the first one:

`a=(T)/(m_(10) )`

`W_(30) - T = m_(30)((T)/(m_(10) )   )`

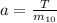
Replacing all values and solving for T:

`30N - T = 3.06kg(T)/(1.02kg) \\30N - T = 3T\\30N=3T + T\\30N = 4T\\(30N)/(4) =T = 7.5N`

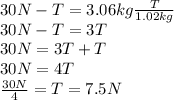
Therefore, the tension in the string has a force of 7.5N, which is less than 30N.

Among the options we have:

• T=10N
• T=20N
• T<30N
• T>30N

Answer 2

T=7.4 N hence T<30 N

Step-by-step explanation:

The figure is likely to be similar to the one attached. Writing the equation for forces we have

F-T=Fa/g where F is the force, T is tension, a is acceleration and g is acceleration due to gravity. Substituting the figures we have the first equation as

30 N - T = (30/9.81)a

Also, we know that T=F*a/g and substituting 10N for F we obtain the second equation as

T = (10/9.81)a

Adding the first and second equations we obtain

30 = 4.077471967

a Hence

`a=\frac {30}{4.077471967}=7.3575 m/s^(2)`

and T=a hence

T is approximately 7.4 N