Question

Solve the simultaneous equation:

y=3x+5

y=4x^2 +x

give your answer correct to 2 decimal places.

Answer 1

I don't approximate. To me that's like turning a correct answer into a wrong answer.

`y = 3x+5`

`y = 4x^2 + x`

`3x + 5 = 4x^2 + x`

`0 = 4x^2 - 2x - 5`

`x = \frac 1 4 (1 \pm √(1^2 - (4)(-5)))`

`x = \frac 1 4 (1 \pm √(21))`

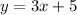
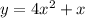
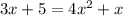
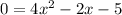
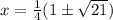
So there are two values for x. Each has an associated y. Since our quadratics have integer coefficients, the pair of ys, like the pair of xs, will be quadratic conjugates:

`y_+ = 3x_++5 = \frac 3 4(1 + √(21)) + 5 = \frac 1 4(23 + 3√(21))`

`y_- = 3x_- +5 = \frac 3 4(1 - √(21)) + 5 = \frac 1 4(23 - 3√(21))`

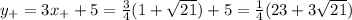
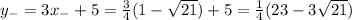
Answer:

`(x,y) = \left( \frac 1 4 (1 + √(21)), \frac 1 4(23 + 3√(21))\right) \textrm{ or } \left( \frac 1 4 (1 - √(21)), \frac 1 4(23 - 3√(21))\right)`

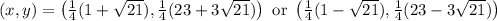
You're on your own for the calculate work.