Question

the population of deer in a park was 250. for 5 years, the population grew by 3% per year, continuously compounded. what was the population at the end of the 5 year period according to the exponential growth function? round your answer down to the nearest whole number, and do not include units.

Answer 1

Answer: 290

Explanation:

Answer 2

Answer: 290

Explanation:

Exponential growth equation to find the values after t years:

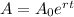`A=A_0e^(rt)`, where
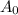`A_0` is the initial value and r is the rate of growth ( in decimal).

As per given , we have

`A_0=250` , r= 3% per year= 0.03 and t= 5 years

Then, the population at the end of the 5 year period will be :-

`A=(250)e^(0.03*5)\\\\= 250*(1.16183424273)\\\\=290.458560682\approx290`

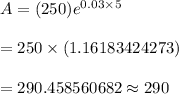
Hence, the population at the end of the 5 year period = 290