Question

the path if an arrow released from a bow can be modeled by y=-0.04 x squared +4x + 3 where x is the horizontal distance (in feet) and y is the vertical distance in feet find and interpret the coordinates of the vertex

Answer 1

The vertex is at the point (50,103). The arrow will reach the highest point 50 feet horizontal distance and 103 feet vertical distance from where it was launched.

Explanation:

The equation of a parabola is given by:

`y=ax^2+bx+c`

The vertex is the maximum or minimum value of the parabola

In this case, we have the following parabola:

`y=-0.04 x^2+4x + 3`

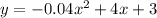
where

a=-0.04

b=4

c=3

The x-coordinate of the vertex can be found by the formula:

`x=(-b)/(2a)`

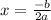
Then, we find the x-coordinate by replacing the values of a nd b:

`x=(-b)/(2a) \\ x=(-(4))/(2* (-0.04)) \\ x=50`

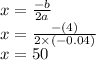
Next, we replace the value of x in the parabola equation:

`y=-0.04 x^2+4x + 3 \\ y =-0.04* 50^2+4* 50 + 3 \\ y =-100+200+ 3 \\ y=103`

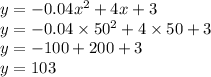
The vertex is at the point (50,103)