Answer:
14°
Explanation:
Here we need to use the theorem, which states:
"An angle formed by two secants is one-half the difference of its intercepted arcs"
In this case, the angle created is 35°, and the intercepted arcs are XZ and VW = 84°.
According to this theorem, we have
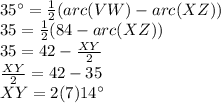
Therefore, according to the theorem, the arc XZ is 14°.