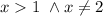Domain:
f(x) has a denominator, which can't be zero. So, its domain is given by
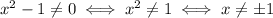
g(x) has a denominator as well. Moreover, it has a root. So, the content of the root can't be negative:
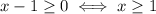
And the denominator can't be zero:
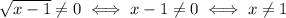
So, the domain is
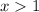
Composition:
We have
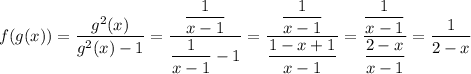
The domain of this function is
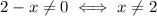
But we also have to remember about the domain of g(x): if g(x) is undefined, we can't compute f(g(x))!
So, the domain of f(g(x)) is