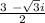Answer:
x is
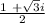 AND
AND
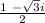
y =
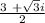 And
And
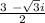
Explanation:
Given two equations are :
y = x² + 2 And
y = x + 1
So, the equation can be written as
x² + 2 = x + 1
Or, x² - x + ( 2 - 1) = 0
Or, x² - x + 1 = 0
This is in the form of quadratic equation
So, Roots of equation x be :
x =
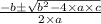
Or, x =

Or , x =

Hence the two value of x is
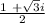 AND
AND
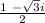
So , y =
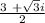 And
And