Question

If x = 3 is a zero of the polynomial function f(x) = 2x^3+ x2 - 25x + 12, which of the following is another zero of f(x)?

x= -3
x=4
x= -4
x = 12

Answer 1

From the given four options, another factor of polynomial
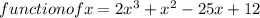`function of x=2 x^(3)+x^(2)-25 x+12` is x = -4.

Solution:

Given that x = 3 is a zero of the polynomial function
`x=2 x^(3)+x^(2)-25 x+12`

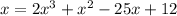
Need to check if any other zeros is present in four given option. Let us understand what is zero of a polynomial. A zero for polynomial is that value of variable x for which dependent function of (x) = 0.

So we need to check for all four values of x,

Corresponding value of polynomial
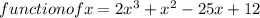`function of x=2 x^(3)+x^(2)-25 x+12` and if it is equal to 0 that that value of x is zero of f of x.

On substituting x= -3, we get

`\begin{array}{l}{2(-3)^(3)+(-3)^(2)-25(-3)+12} \\\\ {\Rightarrow -54+9+75+12=42}\end{array}`

As function of -3 = 42, which is not equal to 0,

So x= -3 is not a zero of polynomial
`\rightarrow 2 x^(3)+x^(2)-25 x+12`

On substituting x = 4, we get

`\begin{array}{l}{\rightarrow 2(4)^(3)+(4)^(2)-25(4)+12} \\\\ {\Rightarrow (2 * 64)+16-100+12} \\\\ {\Rightarrow 128+16+12-100=56}\end{array}`

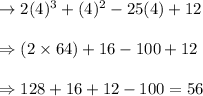
As function of 4 = 56, which is not equal to 0,

So x= 4 is not a zero of polynomial
`\rightarrow 2 x^(3)+x^(2)-25 x+12`

On substituting x = -4, we get

`\begin{array}{l}{\rightarrow 2(-4)^(3)+(-4)^(2)-25(-4)+12} \\\\ {\Rightarrow (2 *(-64))+16+100+12} \\\\ {\Rightarrow -128+16+12+100=-128+128=0}\end{array}`

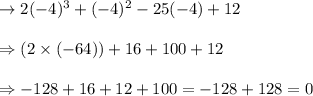
As function of -4 = 0 , so x = -4 is a zero of a zero of polynomial
`function of x=2 x^(3)+x^(2)-25 x+12`

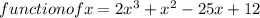
On substituting x = 12, we get

`\begin{array}{l}{function of 12=2(12)^(3)+(12)^(2)-25(12)+12} \\\\ {\Rightarrow function of 12=1728+144-300+12} \\\\ {\Rightarrow function of 12=1584}\end{array}`

As function of 12 = 1584, which is not equal to 0,

So, x= 12 is not a zero of polynomial
`function of x=2 x^(3)+x^(2)-25 x+12`

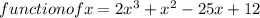
Therefore, the another zero is x=-4.