Question

A man with a mass of 65 kg skis down a frictionless hill that is5.0m high. At the bottom of the hill the terrain levels out. As the man reaches the horizontal section, he grabs a 20-kgbackpack and skis off a 2.0m-high ledge. At what horizontaldistance from the edge of the ledge does the man land?

I understand that his velocity as he picks up the backpack is9.9 m/s but I don't know how to get how far he went.

Answer 1

6.14m

Step-by-step explanation:

As the man skis from top to the bottom of the hill, assuming that there's no friction, his potential energy would be converted to kinetic energy:

By law of energy conservation:

`E_k = E_p`

`(mv^2)/(2) = mgy`

`v^2 = 2gy`

`v = √(2gy)`

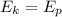
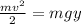
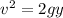
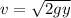
Let's g = 10 m/s2 and y = 5m. Then his speed when he reaches the horizontal section is

`v = √(2*10*5) = 10m/s`

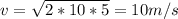
When he grabs the 2kg backpack, momentum conservation dictates is speed after

`mv = Mv_2`

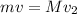
where m = 65 kg is the man mass before the grabbing. M = 65 + 2 = 67 kg is the total mass of the man and the bag after grabbing.

`v_2 = v(m/M) = 10(65/67) = 9.7 m/s`

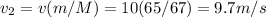
When he drops from a 2 m ledge, suppose he was skiing perfect horizontally before, then his initial vertical speed would be 0. Gravity g = 10 m/s is the only vertical acceleration that takes him down 2m. Since we have

`s = (gt^2)/(2)`

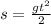
where s = 2 m is the distance covered by gravitational acceleration g = 10m/s. Then the time it takes is

`t^2 = (2s)/(g) = (4)/(10) = 0.4`

`t = √(0.4) = 0.632 s`

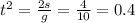
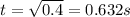
This is also the time it takes for him to travel horizontally across with speed of 9.7 m/s

`s_h = v_2t = 9.7*0.632 = 6.14m`