Question

Water flowed out of a tank at a steady rate. A total of 18 and one-half gallons flowed out of the tank in 4 and one-fourth hours. Which expression determines the quantity of water leaving the tank per hour?

StartFraction 17 over 4 EndFraction divided by StartFraction 36 over 2 EndFraction
StartFraction 36 over 2 EndFraction divided by StartFraction 17 over 4 EndFraction
StartFraction 17 over 4 EndFraction divided by StartFraction 37 over 2 EndFraction
StartFraction 37 over 2 EndFraction divided by StartFraction 17 over 4 EndFraction

Answer 1

D

37/2 divided by 17/4

Step-by-step explanation:

edge 2020

Answer 2

StartFraction 37 over 2 EndFraction divided by StartFraction 17 over 4 EndFraction

Step-by-step explanation:

This problem deals with solving and find the rate at which water flowed out of the tank.

Quantity of water that flowed out of the tank = 18
`(1)/(2)` gallons =
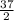`(37)/(2)`gallons

Time taken = 4
`(1)/(4)`hr =
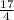`(17)/(4)`hr

Now to find the rate;

Rate of water flow =
`(Quantity of water )/(Time taken)`

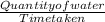
Rate of water flow =
`(37)/(2)` /
`(17)/(4)`

=
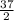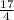
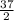`(37)/(2)` x
`(4)/(17)`

=
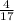
`(74)/(17)`gallons/hr