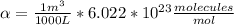Question

Let's write that m = molarity in units of moles/liter and n = number density = N/V, the number of molecules divided by the volume they are in, in units of molecules/m3. Since m and n must be proportional, we expect there is an equation n = αm where α is some constant. Find the numerical value of α and its units (keeping "moles" and "molecules" as units).

Answer 1

`\alpha=6.022*10^(20)(m^3 * molecules)/(L * mol)`

Step-by-step explanation:

Hi, the question states that there is a proportional relation between m (molarity) and n (number density), by following formula:

`m=\alpha*n`

The units of alpha (
`\alpha`) must help to balance the units of m and n.

1) First in both sides there are volume units liter and m3. So we need to express all volume in the same unit. Knowing that:
`1 m^3=1000 L`

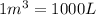
2) We also need to find a relation between mol and molecules. The relation is given by the Avogadro's number:
`A=6.022*10^(23) (molecules)/(mol)`

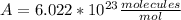
With this two numbers we can balance the units and find the value of
`\alpha` :

`\alpha=(1 m^3)/(1000 L)*6.022*10^(23)(molecules)/(mol)`

`\alpha=6.022*10^(20)(m^3 * molecules)/(L * mol)`