Question

Your engineering firm is asked to specify the maximum load for the elevators in a new building. Each elevator has mass 500 kg when empty and maximum acceleration 2.25 m/s^2. The elevator cables can withstand a maximum tension of 19.6 kN before breaking. For safety, you need to ensure that the tension never exceeds two-thirds of that value. What do you specify for the maximum load?How many 75.0-\rm kg people is that?

Answer 1

a) 584.39 kg

b) 7

Step-by-step explanation:

Given;

Mass of the elevator, m = 500 kg

Maximum acceleration, a = 2.25 m/s²

Maximum tension = 19.6 kN

Allowable tension =
`\frac{\textup{2}}{\textup{3}}*\textup{Maximum tension}` =
`\frac{\textup{2}}{\textup{3}}*\textup{19.6}`

= 13.067 kN

a)let the maximum load be 'x' Now,

T(max) = mass × acceleration

13.067 kN = ( 500 + x ) × ( g + a ) [maximum acceleration will be when lift moves upward i.e (g + a )]

or

⇒ 13.067 × 10³ N = ( 500 + x ) × ( 9.8 + 2.25 )

or

⇒ 13.067 × 10³ N = ( 500 + x ) × 12.05

or

⇒ 13.067 × 10³ N = 6025 + 12.05x

or

⇒ 13067 - 6025 = 12.05x

or

⇒ 12.05x = 7042

or

⇒ x = 584.39 kg

b) Mass of a person = 75.0 kg

Number of 75.0 kg persons that can be allowed =
`\frac{\textup{Maximmum load}}{\textup{Mass of each person}}`

=
`\frac{\textup{584.39}}{\textup{75}}`

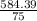
= 7.79

to be on safer side, rounding off to nearest lowest integer i.e 7