Answer:
Grade A:
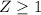
Grade B:

Grade C:

Grade D:
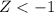
Explanation:
Problems of normally distributed samples can be solved using the Z score table.
The Z score of a measure represents how many standard deviations it is above or below the mean of all the measures.
Each Z score has a pvalue. This represents the percentile of the measure.
In this problem, we have that:
The upper 16% of the class get A grades. The upper 16% has a pvalue of at least 100% = 16% = 84% = 0.84. This is
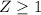 .
.
The middle 34% of the class get B grades. The middle 34% has a pvalue of at least 84%-35% = 50% = 0.5 and at most 0.84. This is
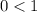 .
.
Those between a pvalue of 0.5-0.34 = 0.16 and 0.5 get get grade C.
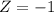 has a pvalue of 0.16. So a grade C is in the interval
has a pvalue of 0.16. So a grade C is in the interval
 .
.
Those with Z lesser than -1 get grades D and F