Question

Finding the Domain of a Square Root Function

Consider the function f(x) = 5x - 5+1
Which inequality is used to find the domain?
5x-420
5x - 5+120
5x20
5x -520
DONE

Answer 1

The inequality is
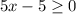`5x-5\geq 0` or
`x\geq 1`

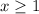
Explanation:

The correct question is

Consider the function f(x)=sqrt(5x-5)+1 which inequality is used to find the domain?

we know that

The square root function is defined only for the positive values including 0.

we have

`f(x)=√(5x-5)+1`

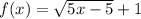
so

The term inside the square root must be greater than or equal to zero

`5x-5\geq 0`

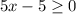
solve for x

Factor 5

`5(x-1)\geq 0`

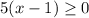
Simplify

`(x-1)\geq 0`

`x\geq 1`

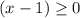
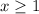
The value of x must be greater than or equal to 1