Answer:
a) 0.1587
b) 0.0475
c) 0.7938
Explanation:
Let's start defining our random variable.
X : ''Thickness (in mm) of ancient prehistoric Native American pot shards discovered in a Hopi village''
X is modeled as a normal random variable.
X ~ N(μ,σ)
Where μ is the mean and σ is the standard deviation.
To calculate all the probabilities, we are going to normalize the random variable X.
We are going to call to the standard normal distribution ''Z''.
[(X - μ) / σ] ≅ Z
We normalize by subtracting the mean to X and then dividing by standard deviation.
We can find the values of probabilities for Z in a standard normal distribution table.
We are going to call Φ(A) to the normal standard cumulative distribution evaluated in a value ''A''
a)

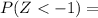 Φ(-1) = 0.1587
Φ(-1) = 0.1587
b)
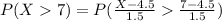
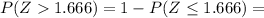
1 - Φ(1.666) = 1 - 0.9525 = 0.0475
c)
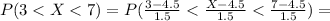
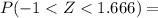 Φ(1.666) - Φ(-1) = 0.9525 - 0.1587 = 0.7938
Φ(1.666) - Φ(-1) = 0.9525 - 0.1587 = 0.7938