Question

A parabola with vertex (h, k) and a vertical axis of symmetry is modeled by the equation y - k = a(x - h)2. Determine the vertex for a parabola modeled by y = (x ? 5)2 + 8 A) (5, 8) B) (?5, 8) C) (5, ?8) D) (?5, ?8)

Answer 1

B.
`(?5,8)`

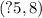
Explanation:

We have been given a parabola with vertex (h, k) and a vertical axis of symmetry is modeled by the equation
`y-k = a(x-h)^2`.

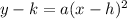We are also given a parabola
`y=(x?5)^2+8`.

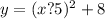Let us convert our given parabola equation in axis of symmetry equation as shown below:

`y=(x?5)^2+8`

`y-8=(x?5)^2+8-8`

`y-8=1(x?5)^2`

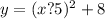
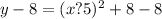
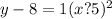
Upon comparing our equation with equation
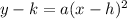`y-k = a(x-h)^2`, we can see that
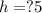`h=?5` and
`k=8`.

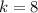Therefore, the vertex of the parabola is
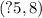`(?5,8)` and option B is the correct choice.