Question

HELP ME PLS very hard

Answer 1

∠XYZ = 72.9°

Explanation:

To find the size of an angle in a right-angled triangle, we can use the trigonometric ratios.

In the definitions of trigonometric ratios, the sides of a triangle are named relative to a particular angle, so that the side opposite to that angle is called 'opposite', the side beside the angle is called 'adjacent', and the side opposite to the 90° (right) angle is called the 'hypotenuse'.

In this triangle:

• opposite ⇒ XZ

• adjacent ⇒ XY

• hypotenuse ⇒ YZ

The trigonometric ratios are as follows:

`\boxed{\mathrm{sin \theta = (opposite)/(hypotenuse), \: cos \theta = (adjacent)/(hypotenuse), \: tan \theta = (opposite)/(adjacent)}}`,

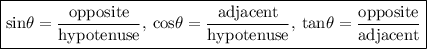where
`\theta` is the main angle.

As we can see in the diagram, the lengths of the opposite and adjacent sides are given. Therefore, we have to use the formula for
`\mathrm{tan \theta}`:

`\mathrm{tan \theta = (opposite)/(adjacent)}`

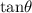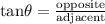
In this case,
`\theta` is angle XYZ.

⇒
`tan\theta = (13)/(4)`

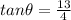
To solve for
`\theta`, take
`tan^(-1)` of both sides:

⇒
`\theta = tan^(-1)((13)/(4))`

⇒
`\theta = \bf 72.9`

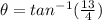
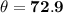
∴ Angle XYZ = 72.9°