Question

A model for the movement of a stock supposes that if the present price of the stock is s, then, after one period, it will be either us with probability p or ds with probability 1 − p. Assuming that suc- cessive movements are independent, approximate the probability that the stock’s price will be up at least 30 percent after the next 1000 periods if u = 1.012,d = 0.990, and p = .52.

Answer 1

`P(X\geq 470)=0.9991`

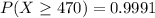
Explanation:

Present price of stock is s, if x is the times that the stock increases (by u) among the 1000 periods we can calculate the price after 1000 periods as follows:

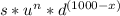`s*u^n*d^((1000-x))` note that if the price increase n periods, so it should decreases in the other 1000-x periods.

We need that the price be 30% higher or 1.3 times the initial price. That requirement is expressed as follows:

`s*u^n*d^((1000-x))>1.3s`

applying properties of exponents and reorganizing.

`d^(1000)((u)/(d))^x>1.3`

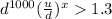
solving for x

`1000 log(d)+ x log ((u)/(d))>log(1.3)`

`x >(log(1.3)-1000 log(d))/(log ((u)/(d)))`

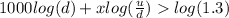
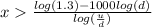
Using the values given d= 0.99 and u=1.012

`x > 469.208967`

So, we need at least 470 increase periods

Now we can calculate the probability of have 470 increase periods or more, taking into account that the distribution of x is binomial, the period can be and increase period with 0.52 of probability and we have 1000 total trials.

The formula for the binomial cumulative probability function is

`F(x;p,n) = \Sigma_0^x \left(\begin{array}{c}n&i\end{array}\right)p^i(1-p)^(n-i)`

With this formula we can calculate the probability of obtain x successful trials or less (
`P(X\leq x)`). There, p is the probability of success (probability of increase period in this case), x is the maximum number of successful trials, n the number of total trials. We should calculate F with x=470, p=0.52 and n= 1000. The result is
`P(X\leq x)`, but we need
`P(X\geq x)` so we can calculate that probability as

`P(X\geq x)=1-P(X\leq x)`

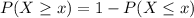
In order to calculate the cumulative function we can use excel function BINOM.DIST

BINOM.DIST(x,trials,probability,cumulative)

BINOM.DIST(470,1000,0.52,TRUE)

We obtain that
`P(X\leq 470)=0.00087`, so
`P(X\geq 470)=1-0.00087=0.9991`