Question

The Grist Mill just paid a dividend of $1.46 per share on its stock. The dividends are expected to grow at a constant rate of 3.5 percent per year, indefinitely. What will the price of this stock be in 4 years if investors require an annual return of 15 percent?Group of answer choices

Answer 1

$15.07

Step-by-step explanation:

`P4=(D5)/((ke-g))`

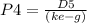
Where,

P4 is the price after 4 years

Ke is the required return = 15.00%

g is the growth rate = 3.5%

D5 is dividend at the end of year:

`=Dividend\ per\ share*(1+g)^(t)`

`=1.46*(1.035)^(5)`

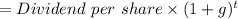
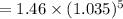
= 1.7340

Therefore,

`P4=(1.7340)/((15\ percent-3.5\ percent))`

`P4=(1.7340)/(11.5\ percent)`

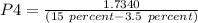
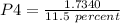
= $15.07

Hence, the price of this stock be in 4 years if investors require an annual return of 15 percent is $15.07.