Answer:

Step-by-step explanation:
There is no friction in the physical system. Thus, according to the law of conservation of energy, recall that the object is released from rest:
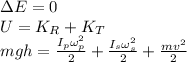
Recall that the moment of inertia of a sphere is
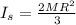 . The angular speed of the pulley is
. The angular speed of the pulley is
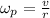 and the angular speed of the sphere is
and the angular speed of the sphere is
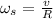 . So, we replace:
. So, we replace:
