Question

Hospital sells raffle tickets to raise fund for new medical equipment. Last year, 2000 tickets were sold for $24 each. The fund-raising coordinator estimates that for every $1 decrease in price, 125 more tickets will be sold 1) What decreases in price will maximize the revenue? 2) What is the price of a ticket that will maximize the revenue? 3) What is the maximum revenue?​

Answer 1

1) Price decrease = $4; 2) new price = $20; 3) maximum revenue = $50 000

Explanation:

The hospital sold 2000 tickets for $24 each

Revenue = price per ticket × number of tickets sold

Let x = change in price

New price = 24 - x

New number of tickets sold = 2000 + 125x

1) Calculate change in price to maximize revenue

y = (24 - x)(2000 + 125x)

y = 48 000 + 1000x - 125x²

y = -125x² + 1000x + 48 000

a = -125; b = 1000; c = 48 000

The vertex is at

`x = -(b)/(2a) = -(1000)/(2(-125))= (1000)/(250) = \mathbf{4}`

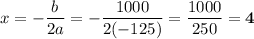
A price decrease of $4 will maximize revenue.

2) New ticket price

Original price = $24

Price change = - 4

New price = $20

A ticket price of $20 will maximize revenue.

3) Maximum revenue

Ticket price = $20

No of tickets sold = 2000 + 125(4) = 2000 + 500 = 2500

Revenue = 2500 × $20 = $ 50 000

The maximum revenue is $50 000.

The graph below slows the relation between the price drop and total revenue. A price drop of $4 results in a maximum revenue of $50 000.