Question

A hypothesis will be used to test that a population mean equals 8 against the alternative that the population mean does not equal 8 with known variance σ. What are the critical values for the test statistic
`Z_0` for the significance level of 0.10? Round your answer to two decimal places.

Answer 1

The required critical values is ±1.65

Explanation:

Consider the provided information.

We have given that the significance level is 0.10

Therefore, α=0.10

This is a two tailed test.

The Z critical value is:
`Z_{(\alpha)/(2)}`

`Z_{(\alpha)/(2)}=Z_{(0.10)/(2)}=0.05`

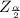
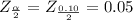
Now by using the table we can find the required value.

`Z_{(\alpha)/(2)}=1.645`

`-Z_{(\alpha)/(2)}=-1.645`

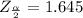
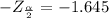
Hence, the required critical values is ±1.65