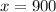Question

One evening 1500 concert tickets were sold for the Fairmont Summer Jazz Festival. Tickets cost $25 for a covered pavilion seat and $15 for a lawn seat. Total receipts were $28500. How many of each type of ticket were sold? Use substitution or elimination.

Answer 1

To find out how many of each type of ticket were sold at the Fairmont Summer Jazz Festival, we created two equations based on the given facts and solved them using the substitution method. We found out that 600 covered pavilion tickets at $25 each and 900 lawn tickets at $15 each were sold.

Step-by-step explanation:

To solve the problem, we need to determine how many covered pavilion seats and lawn seats were sold for the Fairmont Summer Jazz Festival when the total receipts amounted to $28,500. Let's denote x as the number of covered pavilion seats sold and y as the number of lawn seats sold. We have two equations based on the given information:

• Equation for the total number of tickets sold: x + y = 1500
• Equation for the total amount of money made: 25x + 15y = 28500

We can use substitution or elimination to solve these equations. Here, we will opt for the substitution method.

1. Solve the first equation for x: x = 1500 - y.
2. Substitute this expression for x into the second equation: 25(1500 - y) + 15y = 28500.
3. Simplify and solve for y: 37500 - 25y + 15y = 28500, so 10y = 9000, which means y = 900.
4. Substitute y = 900 into the expression for x: x = 1500 - 900, so x = 600.

Therefore, 600 covered pavilion tickets and 900 lawn tickets were sold.

Answer 2

Tickets of lawn seat sold = 900

Tickets of pavilion seat sold = 600

Step-by-step explanation:

Let
`x` be the no. of lawn seats and
`y` be the no. of pavilion seats.

According to the given question,

`x + y = 1500` ----eq 1 and

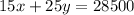`15x + 25y = 28500` ---- eq 2

After obtaining the two equations we can solve this by either substitution or elimination.

By substitution, put

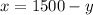`x = 1500 - y` from eq 1 to eq 2, and solve for y, which gives

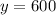`y = 600` and then substitute this value in eq 1 to get

`x = 900`

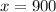
By elimination, make the coefficient of one variable say x equal in both equations, for this multiply eq 1 with 15

now eq 1 becomes

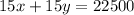`15x + 15y = 22500` subtract this equation from eq 2 to get

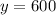`y = 600` and substitute this value in eq 1 to get

`x = 900`