Answer:
a)
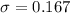
b) We need a sample of at least 282 young men.
Explanation:
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by
, the zscore of a measure X is given by

This Zscore is how many standard deviations the value of the measure X is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
(a) What standard deviation must x have so that 99.7% of allsamples give an x within one-half inch of μ?
To solve this problem, we use the 68-95-99.7 rule. This rule states that:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviations of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we want 99.7% of all samples give X within one-half inch of
 . So
. So
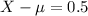 must have
must have
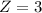 and
and
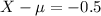 must have
must have
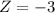 .
.
So

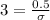


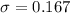
(b) How large an SRS do you need to reduce the standard deviationof x to the value you found in part (a)?
You know from government data that heights of young men are approximately Normal with standard deviation about 2.8 inches. This means that

The standard deviation of a sample of n young man is given by the following formula
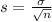
We want to have
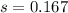
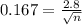
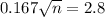
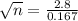
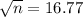
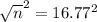

We need a sample of at least 282 young men.