Question

A DC10 airplane travels 3000 km with a tailwind in 3 hr. It travels 3000 km with a headwind in 4 hr. Find the speed of the plane and the speed of the wind. Use substitution or elimination to solve.

Answer 1

The speed of plane is 875 km/h and speed of wind is 125 km/hr

Explanation:

Assuming v the speed of plane and w the speed of wind

Then, the overall speed will be given as (v+w)

The speed is calculated by the formula;

`$\frac{\text { Distance }}{\text { Time }}$`

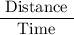
For tailwind, given distance travelled is 3000 km in 3 hrs

Putting the values in the formula;

(v+w) =
`$(3000)/(3)$`

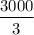
(v+w) = 1000 ……eqn (1)

Similarly, for headwind, given distance travelled is 3000 km in 4 hrs

(v-w) =
`$(3000)/(4)$`

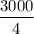
(v-w) = 750 ……eqn (2)

Adding (1) and (2), we get

2v = 1750

v = 875 km/hr

putting value in eqn (1), we get: w = 125 km/hr

Therefore, the speed of plane is 875 km/h and speed of wind is 125 km/hr.