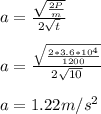Answer:
a-)
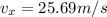
b-)

c-)
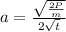
d-)
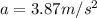
e-)
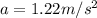
Step-by-step explanation:
First, lay out the given data:
P = 3.6 x 10^4 W
m=1200 kg
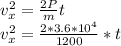
a)What is the car's speed at t=11 s ?

b) What is the car's speed at t=18 s ?
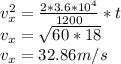
c) Find a symbolic expression, in terms of P, m, and t, for the car's acceleration at time t.
An expression for the acceleration can be defined by finding the derivative of the velocity equation:
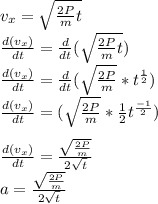
d) Evaluate the acceleration at t=1.0 s
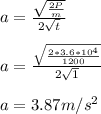
e) Evaluate the acceleration at t=10 s