Answer:
1.76% of the rolls are rejected.
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
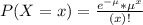
In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
In this problem, we have that:
The mills at a carpet company produce, on average, one flaw in every 500 yards of material produced; the carpeting is sold in 100-yard rolls. This means that for each 100 yard rolls, there are expected 0.2 failures. So
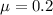 .
.
If the number of flaws in a roll follows a Poisson distribution and the quality-control department rejects any roll with two or more flaws, what percent of the rolls are rejected?
This is
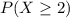 .
.
Either the number of failures is lesser than two, or it is two or greater. The sum of the probabilities of these events is decimal 1.
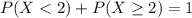
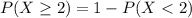
In which
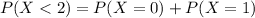 .
.
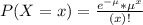
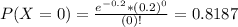

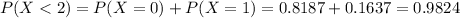 .
.
Finally
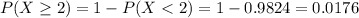
1.76% of the rolls are rejected.