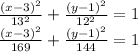Question

An ellipse has a center of (3, 1), a focus of (8, 1), and a directrix of x = 36.8. Which is the equation of the ellipse?

Answer 1

the first option is correct

Explanation:

Answer 2

The equation of the ellipse is
`((x-3)^2)/(169) +((y-1)^2)/(144)=1`

Explanation:

The equation of the ellipse is given by:

`((x-x_0)^2)/(a^2) +((y-y_0)^2)/(b^2)=1`

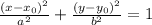
where:

Center of the ellipse is (x₀,y₀)

Vertices: (x₀±a,y₀)

c: distance from the center to the focus
`c=√(a^2-b^2)`

Eccentricity
`e=(c)/(a)`

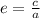
Directrix=
`x_0 + (a^2)/(c)`

So we can obtain the values:

c=(8, 1)-(3, 1)=8-3= (5,0)=5

x₀= 3

y₀= 1

The directrix is x = 36.8

`36.8 = x_0 + (a^2)/(c)\\ 36.8 = 3 + (a^2)/(5)\\  36.8 -3=  (a^2)/(5)\\ 33.8* 5= a^2\\ 169=a^2\\ √(169) =a\\ a=13`

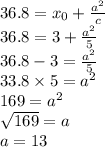
Then, we have to obtain b:

`c=√(a^2-b^2)\\ c^2=a^2-b^2\\ b^2=a^2-c^2\\ b^2=13^2-5^2\\ b^2=169-25\\ b=√(144) \\ b=12`

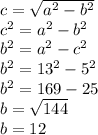
The equation of the ellipse is:

`((x-3)^2)/(13^2) +((y-1)^2)/(12^2)=1 \\ ((x-3)^2)/(169) +((y-1)^2)/(144)=1`