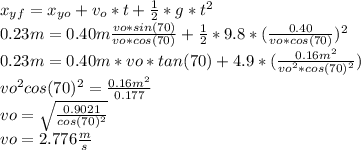Question

An archer fish launches a droplet of water from the surface of a small lake at an angle of 70° above the horizontal. He is aiming at a juicy spider sitting on a leaf 40 cm to the east and on a branch 23 cm above the water surface. The fish is trying to knock the spider into the water so that the fish can eat the spider. (a) What must the speed of the water droplet be for the the fish to be successful?

Answer 1

a). v=2776 m/s

Step-by-step explanation:

The speed of the water droplet for the fish be successful is

Taking the distance in axis 'x' and 'y'

`x_(tx)=40cm(1m)/(100cm)=0.40m\\x_(ty)=23cm(1m)/(100cm)=0.23m`

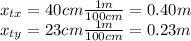
The time is the velocity in axis 'x' with the angle 70 so

`t=(0.40m)/(v_(x)*cos(70))`

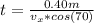
Now using the time in terms of velocity the motion in axis 'y' can find the velocity to be the fish successful

`x_(yf)=x_(yo)+v_(o)*t+(1)/(2)*g*t^(2)\\0.23m=0.40m(vo*sin(70))/(vo*cos(70)) +(1)/(2)*9.8*((0.40)/(vo*cos(70)) )^(2)\\0.23m=0.40m*vo*tan(70)+4.9*((0.16m^(2) )/(vo^(2) *cos(70)^(2) )) \\vo^(2)cos(70)^(2)=(0.16m^(2) )/(0.177)\\vo=\sqrt{(0.9021)/(cos(70)^(2))} \\vo=2.776 (m)/(s)`