Question

Aramis is adjusting a satellite because he finds it is not focusing the incoming radio waves perfectly. The shape of his satellite can be modeled by (x-4)^2=3(y-3) where x and y are modeled in inches. He realizes that the static is a result of the feed antenna shifting slightly off the focus point. Where should the feed antenna be placed?

Answer 1

(4,3.75).

Explanation:

The shape of his satellite can be modeled by the given equation is

`(x-4)^2=3(y-3)` .... (1)

where x and y are modeled in inches.

He realizes that the static is a result of the feed antenna shifting slightly off the focus point. So, we need to find the focus of the given parabola.

If the equation of a parabola is

`(x-h)^2=4p(y-k)` .... (2)

then focus of the parabola is (h,k+p).

On comparing (1) and (2) we get

`h=4,k=3, 4p=3\Rightarrow p=(3)/(4)`

`Focus=(h,k+p)=(4,3+(3)/(4))=(4,3+0.75)=(4,3.75)`

Therefore, the feed antenna should be placed at (4,3.75).

Answer 2

The antenna should be place 0.75 inches above the vertex.

Explanation:

We have the equation of the parabola:

(x-4)²=3(y-3)

The general equation of the parabola is:

(x-x₀)²=4p(y-y₀)

where:

(x₀,y₀) is the vertex of the parabola

p is the focus of the parabola

Hence,

The vertex of the parabola is (4,3)

The focus of the parabola is given by:

`3=4p\\ p=(3)/(4)\\ p=0.75`

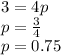
Then, we have to shift the antenna towards the focus point. The focus point would be:

(x₀,y₀+p)=(4,3+0.75)= (4,3.75)

The directrix of the parabola is:

y=y₀-p

y=3-.75=2.25

A graph of the parabola is attached, with its focus point (4.3.75) and its directrix (y = 2.25)