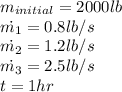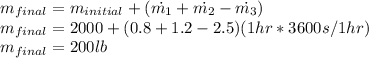Question

Consider a mixing tank initially containing 2000 lbm of liquid water. The tank is fitted with two inlet pipes, one delivering hot water at a mass flow rate of 0.8 lbm/s and the other delivering cold water at a mass flow rate of 1.2 lbm/s. Water exits through a single exit pipe at a mass flow rate of 2.5 lbm/s. Determine the amount of water [lbm] in the tank after one hour.

Answer 1

`m_(final)=200lb`

Step-by-step explanation:

We start with the balance equation for this problem, that is,

`(m_(cv))/(dt) = \sum\dot{m_i}-\sum\dot{m_e}\\(m_(cv))/(dt) = \dot{m_1}+\dot{m_2}-\dot{m_3}\\dm_(cv)=(\dot{m_1}+\dot{m_2}-\dot{m_3})dt`

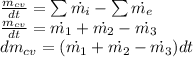
We integrathe this expresión to have the initial and final mass.

`\int\limit^(final)_(initial) = \int\limit^(t=1hr)_(t=0)(\dot{m_1}+\dot{m_2}-\dot{m_3})dt`

`m_(final)=m_(initial)+(\dot{m_1}+\dot{m_2}-\dot_(m_3))t`

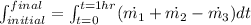
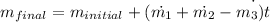
Here we can note remark that

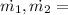`\dot{m_1},\dot{m_2}=` Mass flow rate of hot water and cold water

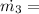`\dot{m_3} =` Mass flow rate of liquit water

Substituting the values

`m_(initial)=2000lb\\\dot{m_1}=0.8lb/s\\\dot{m_2}=1.2lb/s\\\dot{m_3}=2.5lb/s\\t=1hr`

`m_(final)=m_(initial)+(\dot{m_1}+\dot{m_2}-\dot{m_3})\\m_(final)=2000+(0.8+1.2-2.5)(1hr*3600s/1hr)\\m_(final)=200lb\\`