Question

A series circuit has a capacitor of 0.25 × 10⁻⁶ F, a resistor of 5 × 10³ Ω, and an inductor of 1H. The initial charge on the capacitor is zero. If a 12 V battery is connected to the circuit and the circuit is closed at t = 0, determine the charge on the capacitor at t = 0.001 s, at t = 0.01 s, and at any time t. Also determine the limiting charge as t → [infinity].

Answer 1

`q = (3 + e^(-4000 t) - 4 e^(-1000 t))* 10^(-6)`

at t = 0.001 we have

`q = 1.55 * 10^(-6) C`

at t = 0.01

`q = 2.99 * 10^(-6) C`

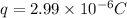
at t = infinity

`q = 3 * 10^(-6) C`

Step-by-step explanation:

As we know that they are in series so the voltage across all three will be sum of all individual voltages

so it is given as

`V_r + V_L + V_c = V_(net)`

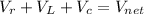
now we will have

`iR + L(di)/(dt) + (q)/(C) = 12 V`

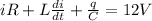
now we have

`1(d^2q)/(dt^2) + (5 * 10^3) (dq)/(dt) + (q)/(0.25 * 10^(-6)) = 12`

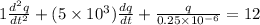
So we will have

`q = 3* 10^(-6) + c_1 e^(-4000 t) + c_2 e^(-1000 t)`

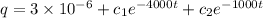
at t = 0 we have

q = 0

`0 = 3* 10^(-6) + c_1  + c_2`

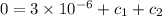
also we know that

at t = 0 i = 0

`0 = -4000 c_1 - 1000c_2`

`c_2 = -4c_1`

`c_1 = 1 * 10^(-6)`

`c_2 = -4 * 10^(-6)`

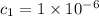
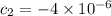
so we have

`q = (3 + e^(-4000 t) - 4 e^(-1000 t))* 10^(-6)`

at t = 0.001 we have

`q = 1.55 * 10^(-6) C`

at t = 0.01

`q = 2.99 * 10^(-6) C`

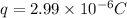
at t = infinity

`q = 3 * 10^(-6) C`