Question

Three glass bulbs, joined by closed stopcocks, have the following volumes and initial pressures of the specified gases.

Bulb A: 200. mL of Kr(g) at 190. torr
Bulb B: 400. mL of H2S(g) at 1.00 atm
Bulb C: 1.00 L of N2(g) at 75.994 kPa

After both stopcocks are opened and the gases allowed to diffuse throughout, what will be the ultimate total pressure?

Answer 1

P = 0.75 atm

Step-by-step explanation:

Using Boyle's law

`{P_A}* {V_A}+{P_B}* {V_B}+{P_C}* {V_C}={P}* {V}`

Given ,

For Bulb A

Pressure = 190 torr

The conversion of P(torr) to P(atm) is shown below:

`P(torr)=\frac {1}{760}* P(atm)`

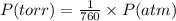
So,

Pressure = 190 / 760 atm = 0.25 atm

Volume = 200 mL

For Bulb B

Pressure = 1 atm

Volume = 400 mL

For Bulb C

Volume = 1.00 L = 1000 mL

Pressure = 75.994 kPa

The expression for the conversion of pressure in KiloPascal to pressure in atm is shown below:

P (kPa) =
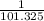`\frac {1}{101.325}` P (atm)

75.994 kPa =
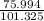`\frac {75.994}{101.325}` atm

Pressure = 0.75 atm

Also, Total volume, V = 200 + 400 + 1000 mL = 1600 mL

Using above equation as:

`{0.25}* {200}+{1.00}* {400}+{0.75}* {1000}={P}* {1600}`

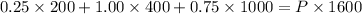
We get, Total pressure, P = 0.75 atm