Question

A ship maneuvers to within 2.46×10³ m of an island’s 1.80 × 10³ m high mountain peak and fires a projectile at an enemy ship 6.10 × 10² m on the other side of the peak, as illustrated. The ship shoots the projectile with an initial velocity of 2.55×10² m/s at an angle of 74.9°.How close to the enemyship does the projectile land? How close (vertically) does the projectile come to the peak?

Answer 1

The distance close to the peak is 597.4 m.

Step-by-step explanation:

Given that,

Distance of the first ship from the mountain
`d=2.46*10^(3)\ m`

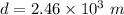
Height of island
`h=1.80*10^(3)\ m`

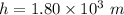
Distance of the enemy ship from the mountain
`d'=6.10*10^(2)\ m`

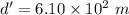
Initial velocity
`v=2.55*10^(2)\ m/s`

Angle = 74.9°

We need to calculate the horizontal component of initial velocity

Using formula of horizontal component

`v_(x)=v\cos\theta`

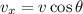
Put the value into the formula

`v_(x)=2.55*10^(2)\cos74.9`

`v_(x)=66.42\ m/s`

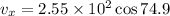
We need to calculate the vertical component of initial velocity

Using formula of vertical component

`v_(y)=v\sin\theta`

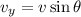
Put the value into the formula

`v_(y)=2.55*10^(2)\sin74.9`

`v_(y)=246.19\ m/s`

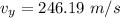
We need to calculate the time

Using formula of time

`t=(d)/(v_(x))`

`t=(2.46*10^(3))/(66.42)`

`t=37.03\ sec`

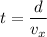
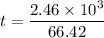
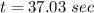
We need to calculate the height of the shell on reaching the mountain

Using equation of motion

`H= v_(y)t-(1)/(2)gt^2`

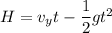
Put the value in the equation

`H=246.19*37.03-(1)/(2)*9.8*(37.03)^2`

`H=2397.4\ m`

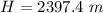
We need to calculate the distance close to the peak

Using formula of distance

`H'=H-h`

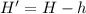
Put the value into the formula

`H'=2397.4-1800`

`H'=597.4\ m`

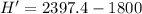
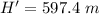
Hence, The distance close to the peak is 597.4 m.