Question

A package falls out of a helicopter that is traveling horizontally at 70 m/s it falls into the water below 8.0 seconds later assuming no air resistance what is the horizontal distance it travels while falling

Answer 1

Answer: D = 560m

Step-by-step explanation: The helicopter is traveling with a velocity of 70m/s in the x-axis, and we know that it takes 8 seconds to fall into the water.

Whem the helicopter "throws" the package, the only equations for the package are the initial velocity, that is the same of the helicopter (70 m/s in the x axis)

and the gravity acceleration in the y axis, but we only care for the horizontal distance, so this does not matter.

Then, knowing that the package travesl for 8 seconds with a velocity of 70m/s in the horizontal direction, the total distance traveled is:

70m/s*8s = 560m

Answer 2

The horizontal distance the package traveled while falling, S = 197.99 m

Step-by-step explanation:

Given,

The horizontal velocity of the helicopter, v = 70 m/s

The time taken by the package to fall into the water is, t = 8.0 s

The initial horizontal component of velocity, Vx = 70 m/s

The initial vertical component of velocity, Vy = 0 m/s

The time of flight is given by the formula

`t=\frac{Vy+\sqrt{Vy^(2) +2gh}}{g}`

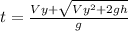
Since Vy = 0 ; solving for h

h = gt²/2 meter

Substituting the given values in the above equation

h = (9.8 x 8²) / 2

= 39.2 m

The horizontal distance traveled while falling is given by the formula

`S=\frac{Vx[Vy+\sqrt{Vy^(2) +2gh}] }{g}`

Since, Vy = 0, equation becomes

`S=(Vx√(2gh) )/(g)`

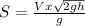
Substituting the values in the above equation

`S=(70√(2X9.8X39.2) )/(9.8)`

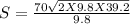
S = 197.99 m

Hence, the horizontal distance the package travels while falling is, S = 197.99 m