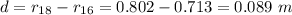Question

A mass spectrometer is being used to separate common oxygen-16 from the much rarer oxygen-18, taken from a sample of old glacial ice. (The relative abundance of these oxygen isotopes is related to climatic temperature at the time the ice was deposited.) The ratio of the masses of these two ions is 16 to 18, the mass of oxygen-16 is 2.66 x 10^-26 kg, and they are both singly charged and travel at 5.15 x 10^6 m/s in a 1.2 T magnetic field. What is the separation between their paths when they hit a target after traversing a semicircle? please show all steps

Answer 1

The path separation is 0.089 m

Solution:

As per the question:

Mass of
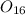`O_(16)`, m = 2.66\times 10^{- 26}\ kg[/tex]

Ratio of the masses of
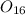`O_(16)` to
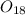`O_(18)`, R = 16:18

Velocity of the masses, v =
`5.15* 10^(6)\ m/s`

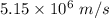
Magnetic field, B = 1.2 T

Now,

The separation between the path after completing a semicircle can be calculated as:

Mass of
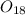`O_(18)`, m' = mR =
`2.66* 10^(- 26)* (18)/(16) = 2.99* 10^(- 26)\ kg`

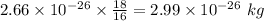
Here, magnetic force provides the necessary centripetal force to traverse the semi-circle:

`F_(B) = F_(c)`

`qvB = (mv^(2))/(r)`

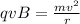
where

`F_(c) = (mv^(2))/(r)`

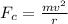
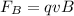`F_(B) = qvB` = Magnetic force

q = e = electronic charge =
`1.6* 10^(- 19)\ C`

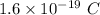
v = Velocity

B = Magnetic field

r = Radius

Now, the radius from the above eqn comes out to be:

`r = (mv)/(qB)`

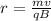
Now, for
`O_(16)[tex]:</p><p>[tex]r_(16) = (mv)/(eB)`

`r_(16) = (2.66* 10^(- 26)* 5.15* 10^(6))/(1.6* 10^(- 19)* 1.2) = 0.713\ m`

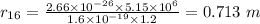
Now, for
`O_(18)[tex]:</p><p>[tex]r_(16) = (m'v)/(eB)`

`r_(16) = (2.99* 10^(- 26)* 5.15* 10^(6))/(1.6* 10^(- 19)* 1.2) = 0.802\ m`

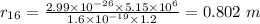
Now, the path separation is given by:

`d = r_(18) - r_(16) = 0.802 - 0.713 = 0.089\ m`