Question

A thin, taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation: y(x,t)=(5.89 cm) sin[(0.0340 rad/cm)x] sin[(50.4 rad/s)t], where the origin is at the left end of the string, the x-axis is along the string, and the y-axis is perpendicular to the string. What is the length of the string?

Answer 1

L=2.77 m

Step-by-step explanation:

Given that

y(x,t)=(5.89 cm) sin[(0.0340 rad/cm)x] sin[(50.4 rad/s)t]

As we know that standard form of wave equation

y = 2A sin kx sin ωt

By comparing the above both equation

2 A = 5.89 cm

A= 2.945 cm

k=0.0340 x 100 m⁻¹= 3.4 rad/m

ω=54.4 rad/s

wavelength given as

λ=2π /k

By putting the values

λ=2 x 3.14 /3.4 = 1.84 m

The length L given as

`\lambda _n=(2L)/(n)`

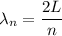
Here n = 3

`1.84=(2L)/(3)`

L=2.77 m