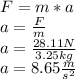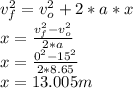Answer:
x=13.005m
Step-by-step explanation:
The kinetic friction μk=0.397 is when the motion is development so:
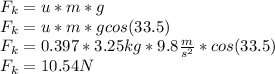
The net force of the motion is the relation of component of block weight acting parallel to ramp and against block's motion

The net force of the motion is :
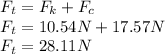
The total force is the relation of mass and acceleration so, can find the acceleration to determinate the distance the block go far after the motion