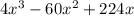Question

Write the polynomial function that models the given situation. A rectangle has a length of 16 units and a width of 14 units. Squares of x by x units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume V of the box as a polynomial function in terms of x.

Answer 1

`4x^3-60x^2+224 x`

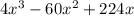
Explanation:

We are given that

Length of rectangle=16 units

Width of rectangle=14 units

We have to write a polynomial function for volume of the box when a square of side x cut from each corner of given box.

Length of new box=16-2x units

Width of new box= 14-2x units

Height of new box=x units

Volume of box=
`L* B* H`

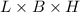
Substitute the values then we get

Volume of new box=
`(16-2x)(14-2x)x`

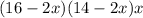
Volume of new box=
`4x^3-60x^2+224 x`

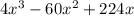
Hence, the volume of the box as a polynomial function is given by

`4x^3-60x^2+224 x`