Question

(3,1) m=0
In standard form

Answer 1

0x + y = 1 is the standard form of (3, 1) with m = 0

Solution:

We have been given a point and slope of an equation and have been asked to write it in the standard form.

The standard form of a line is in the form Ax + By = C where A is a positive integer, and B, and C are integers. The standard form of a line is just another way of writing the equation of a line.

The given point is (3,1) and the slope is 0

To write in standard form we will first write it in point slope form and then rearrange it into a standard from.

The point slope form of line is given as:

`y-y_(1)=m\left(x-x_(1)\right)`

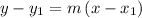
Where "m" is the slope of the line

Here in this problem,
`m = 0 , x_1 = 3 and y_1 = 1`

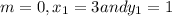
y - 1 = 0(x - 3)

y - 1 = 0

y = 1

since the above equation doesn’t have an ‘x’ term we convert into a standard form as follows:

0x + y = 1

This is the standard form for the given point and slope of a line.