Answer:
D. 54,900
Explanation:
We have been given that the salary of teachers in a particular school district is normally distributed with a mean of $50,000 and a standard deviation of $2,500.
To solve our given problem, we need to find the sample score using z-score formula and normal distribution table.
First of all, we will find z-score corresponding to probability
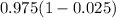 using normal distribution table.
using normal distribution table.
From normal distribution table, we get z-score corresponding is
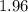 .
.
Now, we will use z-score formula to find sample score as:
 , where,
, where,
 = Z-score,
= Z-score,
 = Sample score,
= Sample score,
 = Mean,
= Mean,
 = Standard deviation
= Standard deviation
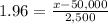
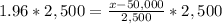

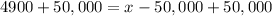
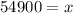
Therefore, the salary of $54900 divides the teachers into one group that gets a raise and one that doesn't.