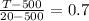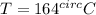Answer:
The center line temperature of the beam is
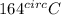
Solution:
As per the question:
Diameter of the cylinder, D = 0.5 m
Radius of the cylinder, r' =
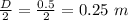
Temperature,
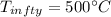
Initial temperature,
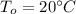
Convection coefficient of heat flow,
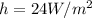
Time, t = 46 min
k =

Now,
Biot no. is given by:

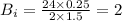
Now, Fourier no. is given by:
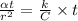
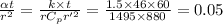
At
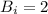 ,
,
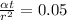
Now, using Heisler chart, the temperature of the beam is given by: